Sebelumnya saya ucapkan terima kasih kepada saudara Muhammad Amsar, asal pertanyaan ini bermula...
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk p/q, dengan q ≠ 0. Misalkan 4 dan 0,25 merupakan bilangan rasional karena dapat dinyatakan dalam bentuk 4/1 dan ¼. Dalam barisan bilangan dapat kita temukan bilangan desimal yang memiliki panjang tak hingga (desimal berulang) sehingga nampak tidak dapat dirasionalkan, semisal 0,272727… dan 0.432432432…. Benarkah bilangan ini tidak dapat diubah dalam bentuk rasional? Mungkin kebanyakan dari Anda sudah tahu bahwa kedua bilangan desimal tadi dapat diubah dalam bentuk desimal seperti halnya 0,333… dapat diubah menjadi 1/3. Bilangan desimal berulang seperti ini biasanya dituliskan dengan notasi pemberian garis atas pada bilangan yang berulang. Setidaknya ada dua metode untuk memecahkannya yaitu:
1. Metode Pembagian
Metode ini sederhana, yaitu mengurangkan suatu bilangan desimal berulang dengan bilangan yang merupakan perkalian kelipatan 10 dengan bilangan tadi.
atau x = 3/11. Dengan metode yang sama didapatkan
2. Metode Deret Konvergen
Metode ini menggunakan limit jumlah deret konvergen. Misalkan bilangan desimal berulang x = 0,272727…, dapat kita nyatakan dalam deret 0,27 + 0,0027 + 0,000027 + …. Deret ini memiliki suku pertama a = 0,27 dan rasio, r = 0,01. Jumlahnya adalah:
Dengan metode yang sama didapatkan
Nah, sekarang bagaimana dengan 0,49999…? Dengan meode pembagian kita dapatkan
Dan didapatkan 0,4999… = 0,5 ???
Kita coba dengan metode Deret konvergen, misalkan 0,4999.. = x = y + z, dengan y = 0,4 dan z = 0,0999…. Nilai z kita dapatkan:
Karena x = y + z maka 0,4999… = 0,4 + 0,1 = 0,5. (hasil yang sama). Jadi kita berkesimpulan 0,499… = 0,5. Mungkin ada yang bertanya kok bisa? Jawabannya adalah suatu bilangan x dapat dinyatakan tidak sama dengan y jika dapat ditemukan suatu bilangan lain diantara x dan y, semisal u, jadi dapat ditulis secara matematis x ≠ y dan x<u<y. Nah adakah bilangan diantara 0,499… dan 0,5? Untuk mencari bilangan di antara dua bilangan dengan n angka penting dibelakang koma, maka bilangan antara itu haruslah memiliki minimal n+1 angka penting dibelakang koma. Misalkan x = 0,3454 dan y = 0,3455, mustahil untuk mendapatkan bilangan antara yang mempunyai kurang atau sama dengan empat angka penting di belakang koma. Jadi bilangan itu pastilah memiliki lima atau lebih angka penting di belakang koma, semisal 0,34541. Nah, 0,499… memiliki tak hingga angka penting di belakang koma, jadi untuk mencari bilangan di antara 0,499… dan 0,5 Anda harus bisa mengejar satu langkah di depan yang namanya “tak hingga” yang sudah barang tentu mustahil.
Kesimpulannya 0,499… = 0,5, meskipun kelihatannya berbeda (=paradoks).

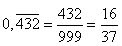



Kak, bagaiamana kalau (1,275000...1)
BalasHapusApakah bisa di rasionalkan???
Bisa. Kalikan saja dengan (10000...0)/(10000...0).
HapusKalau yang Anda maksud dengan "000..." itu sampai tak hingga jumlah nol-nya ya jadinya kontradiksi dengan Anda meletakkan angka 1 di ujungnya. Tak hingga kan tidak memiliki ujung.
Ka kalo 0,12345345345....
BalasHapusItu gimna ya ka