Mana yang Lebih Banyak, Orang Hidup atau Orang Mati?
Melihat laju pertumbuhan penduduk dunia tentunya akan membuat kita geleng-geleng kepala. Mungkin pertanyaan pertama yang terpikir oleh Anda ialah apakah beberapa abad ke depan Bumi masih muat menampung seabrek penduduknya? Lalu terbersit pertanyaan di kepala saya: Mana yang lebih banyak, Orang hidup atau orang yang sudah mati? Sebagai gambaran, berikut grafik jumlah penduduk dunia dari tahun ke tahun.
Jadi menurut Anda, manakah yang lebih banyak?
Saya akan mencari solusinya menggunakan model matematika. sebelumnya, kita ambil asumsi-asumsi berikut untuk mempermudah perhitungan.
- Gunakan skala waktu dalam generasi (+/- 70 tahun)
- Gunakan model diskret dan anggap tiap orang hanya hidup dalam satu selang generasi sehingga pada generasi berikutnya ia dianggap mati. Dengan demikian, jumlah orang yang hidup kita nyatakan dalam f(t) dan jumlah orang yang mati ialah jumlah dari f(0) hingga f(t-1).
- Asumsikan fungsi jumlah penduduk berdasarkan waktu f(t) = t2. Silakan mencoba fungsi lain yang nampaknya sesuai.
Dengan kedua asumsi tadi, kita telah menyederhanakan problem ini sehingga dapat dituliskan sebagai:
 "\textup{orang hidup}=f(t)")
 "\textup{orang mati}=\sum_{n=0}^{t-1}f(n)")
Tentu saja model ini hanyalah suatu pendekatan, namun cukup baik untuk menjawab pertanyaan di atas. Nah, di awal pembuktian kita coba ambil pertidaksamaan orang mati < orang hidup.
%3Cf(t) "\sum_{n=0}^{t-1}f(n)<f(t)")
kita ambil lagi pendekatan integral (lihat di sini) sehingga persamaan di atas menjadi:
%5C,&space;dt+%5Cfrac%7Bf(t-1)%7D%7B2%7D%3Cf(t) "\int_{0}^{t-1}f(t)\, dt+\frac{f(t-1)}{2}<f(t)")
Dengan memasukkan nilai f(t) diperoleh:
%5E2%7D%7B2%7D%3Ct%5E2 "\int_{0}^{t-1}t^2\, dt+\frac{(t-1)^2}{2}<t^2")
%5E2%7D%7B2%7D%3Ct%5E2 "\left [\frac{t^3}{3} \right ]_0^{t-1}+\frac{(t-1)^2}{2}<t^2")
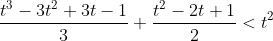
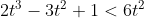
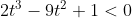
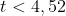
atau jika dibulatkan t < 5.
Kita coba gambarkan tabelnya
| t | 1 | 2 | 3 | 4 | 5 |
| hidup | 1 | 4 | 9 | 16 | 25 |
| mati | 0 | 1 | 5 | 14 | 30 |
Terlihat untuk t > 5 (5 generasi), jumlah orang mati sudah lebih banyak dari orang hidup jika fungsi jumlah penduduk f(t) = t2. Mengingat manusia sudah ada selama puluhan ribu tahun, tentu saja sudah berada pada t yang sangat besar. Silakan analisis fungsi fungsi jumlah penduduk dunia menggunakan regresi kalau masih tidak percaya. Jika Anda hitung dan memasukkan funsinya dalam model di atas saya yakin jumlah orang yang sudah mati lebih banyak daripada jumlah orang yang hidup. Malah jika diteliti dengan seksama, berapapun tanjakan dari fungsi f(t), t10 sekalipun akan ada suatu waktu di mana jumlah orang mati melampaui yang hidup.
[UPDATE]
Berikut adalah koreksi berdasarkan komentar dari Pak Mariano, saya mengucapkan banyak terima kasih atas apresiasinya dan sikap kritisnya terhadap tulisan saya. Saya sengaja hanya menambahkan update di bagian bawah -- tidak memposting ulang, selain karena pemodelan yang lalu setelah saya teliti tidak ada kekeliruan selain pendekatan fungsi yang tidak tepat, tentu saja juga karena proses berpikir itu indah. Sekarang saya akan mengambil fungsi eksponensial satu suku dengan mantissa sembarang yang dapat ditulis f(t) = xt, di mana x kelipatan jumlah penduduk (hidup) tiap masa satu generasi. Jika dimasukkan dalam model menjadi:
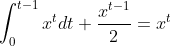
%7D-%5Cfrac%7B1%7D%7B%5Cln(x)%7D+%5Cfrac%7Bx%5E%7Bt-1%7D%7D%7B2%7D=x%5Et "\frac{x^{t-1}}{\ln(x)}-\frac{1}{\ln(x)}+\frac{x^{t-1}}{2}=x^t")
%7D-%5Cfrac%7B1%7D%7B%5Cln(x)%7D+%5Cfrac%7Bx%5Et%7D%7B2x%7D=x%5Et "\frac{x^t}{x\ln(x)}-\frac{1}{\ln(x)}+\frac{x^t}{2x}=x^t")
-x%5Et(2x%5Cln(x))%7D%7B2x%5Cln(x)%7D=%5Cfrac%7B1%7D%7B%5Cln(x)%7D "\frac{2x^t+x^t\ln(x)-x^t(2x\ln(x))}{2x\ln(x)}=\frac{1}{\ln(x)}")
-2x%5Cln(x)%7D "x^t=\frac{2x}{2+\ln(x)-2x\ln(x)}")
-2x%5Cln(x)%7D&space;%5Cright&space;) "t=\log_x \left (\frac{2x}{2+\ln(x)-2x\ln(x)} \right )")
Agar t memiliki nilai, nilai dalam kurung (yang di-log-kan) harus bernilai lebih besar dari nol (ingat log dari bilangan nonpositif tak terdefinisi). Dengan metode komputasi, saya peroleh x ≈ 1,972 dengan kata lain t hanya terdefinisi untuk x < 1,972. Nah,pertanyaannya apakah dalam kenyataan nilai x ini lebih kecil dari pada 1,972? Setelah meninjau data-data jumlah penduduk dunia (dapat dilihat di sini atau di sini). Dengan mengingat asumsi ke-1 saya mengambil kisaran sebagai berikut:
| tahun | jumlah penduduk (trilyun) |
| 1610 | 0,5 |
| 1680 | 0,6 |
| 1750 | 0,72 |
| 1820 | 1,0 |
| 1890 | 1,5 |
| 1960 | 3,1 |
| 2030 | ~9(perkiraan) |
Berdasarkan data belakangan ini diperoleh rasio rata-rata tidak sampai dua kali, apalagi untuk periode yang lebih lama dari 1610. Tentu saja terlihat rasio semakin meningkat juga dan jikalau prediksi pada tahun 2030 sesuai maka rasionya menjadi 3. Mungkin karena belakangan ini tidak ada perang besar dan bangsa-bangsa Asia tengah menggenjot perkembangannya. Well, karena di sini saya mendapat rasionya lebih kecil dari pada 2 dan sedikit lagi cakaran pada kertas saya, saya mengambil kesimpulan jumlah orang mati masih lebih banyak dibanding orang hidup. Tapi mengingat rasio itu cenderung bertambah bisa saja pada suatu masa orang hidup menjadi lebih banyak.
Menarik sekali pemikirannya, sangat kreatif, memikirkan hal-hal yang sederhana tetapi yang tidak pernah terpikirkan orang lain. Sangat patut ditiru oleh para generasi muda Indonesia.
BalasHapusMembaca artikel di atas saya juga punya ide nih:
Bukankah pertambahan penduduk dunia bersifat eksponensial? artinya fungsinya bukan t^2, tapi mungkin lebih tepat lagi adalah fungsi 2^t.
Misalkan kita pakai fungsi f(t)=2^t, saya coba-coba masukkan ke model fungsi integral yang sudah diturunkan oleh paradokster di atas dan saya peroleh bahwa berapapun nilai t ternyata jumlah orang hidup di waktu t, selalu lebih banyak dari pada kalkulasi jumlah orang mati sejak t=0, bahkan berapapun nilai yang dipangkat t (mis 10^t atau 100^t) tetap memberikan hasil yang sama.
Terima kasih atas komentarnya. Anda memang benar, saya keliru, fungsi f(t) memang lebih tepat didekati secara eksponensial. Setelah coba saya hitung untuk f(t)=x^t, jika x<1,972 jumlah orang mati dapat melampaui jumlah orang hidup pada t tertentu. Silakan Anda coba untuk f(t)=1,5^t.
BalasHapusNah, permasalahannya ialah menentukan fungsi f(t) yang sebenarnya. Akan saya cari dengan pemodelan baru dan analisis grafik. Akan saya update jika sudah didapat. nilai 1,972 ini nilai kritis, apabila kita berhasil mendapatkan nilai x ini, problem ini akan terpecahkan. Mohon bantuannya dan sekali lagi terima kasih atas koreksinya..