Buku yang baik adalah buku dengan pengantar yang mampu menjembatani pemahaman kita tentang suatu materi dengan konsep yang ingin dijabarkan oleh buku tersebut. Utamanya buku-buku fisika dan matematika, bila buku tadi memiliki pengantar yang tidak memulai penjelasannya dari sebatas mana pengetahuan kita berarti buku itu memang tidak ditujukan untuk tingkatan kita. Tetapi bila penulis buku mengklaim bukunya sesuai untuk suatu tingkatan akademik dan kita berada di tingkatan yang dimaksud – dengan kemampuan yang cukup pula, tidak juga mengerti dari mana konsep materi si buku bermula, berarti buku itu tergolong buku yang “buruk”.
Ini adalah pengalaman saya saat berkenalan dengan yang namanya persamaan diferensial (PD) sekitar lima tahun lalu. Saya tidak dapat memperoleh buku-buku yang mampu mengantar pemikiran saya dari konsep matematika yang saya pahami menuju konsep persamaan diferensial. Alhasil, saat-saat pertama saya mencoba menghapal saja formulasi matematisnya tanpa memahami konsepnya, dan persamaan diferensial benar-benar mengerikan! Oleh karena itu, di sini saya akan mencoba memberikan sedikit perspektif dan pengantar menuju apa itu persamaan diferensial. Yang akan saya bahas disini tidak lengkap, tetapi lebih ke pengantar menuju pengantar-yang-ada-di-buku-buku-matematika.
Oke, saat kita ingin mempelajari persamaan diferensial, pastinya kita harus sudah memahami kalkulus diferensial. Di sini akan saya mulai dengan fungsi y(x) = C ekx. Turunan fungsi y terhadap x ialah y’(x) = Ck ekx. Dengan demikian kita memperoleh hubungan
Whoiila!! Ini adalah contoh dari persamaan diferensial. Persamaan di atas bernilai benar bila y = C ekx. Mengingat hanya fungsi eksponensiallah yang turunannya sama dengan fungsi awalnya, kita dapat yakin fungsi y(x) = C ekx merupakan solusi tunggal dari PD y’ – ky = 0.
Sekarang tinjau fungsi y(x) = C1 sin(kx), turunan pertamanya ialah y' = C1k cos(kx) dan turunan keduanya y’’ = -C1k2 sin(kx). Dari fungsi awal dan turunan kedua-nya, dapat diperoleh hubungan
Ini juga contoh dari persamaan diferensial orde dua (orde menandakan turunan tertinggi yang terdapat dalam PD). Jadi PD di atas benar jika y = C1 sin(kx). Dengan demikian, y = C1 sin(kx) merupakan salah satu solusi dari PD tadi. Kok salah satu? Ya karena terdapat solusi lain yang mungkin, yakni y = C2 cos(kx). Turunan ke-dua dari y = C2 cos(kx) ialah y’’ = -C2k2 cos(kx) yang bila di substitusikan juga memenuhi PD yang ke-2. Jadi PD itu memiliki dua solusi. Mengingat sifat linear operasi diferensial terhadap penjumlahan dan pengurangan
+v(x)+w(x)+...)'=u'(x)+v'(x)+w'(x)+... "(u(x)+v(x)+w(x)+...)'=u'(x)+v'(x)+w'(x)+...")
Maka kedua solusi yang mungkin itu dapat kita gabungkan menjadi y = C1 sin(kx) + C2 cos(kx). Jika solusi sebenarnya dari suatu problem hanya memuat suku sinus saja, maka C2 sama dengan nol, begitu pula sebaliknya. Jadi solusi dari PD y’’ + k2y = 0 ialah y = C1 sin(kx) + C2 cos(kx).
Kemudian bila kita mengambil fungsi y = C1 sinh(kx), yang turunan ke-duanya ialah y’’ = C1k2 sinh(kx), maka diperoleh hubungan:
Seperti pada contoh sebelumnya, PD ini juga terpenuhi untuk y = C2 cosh(kx), sehingga solusi dari PD ke-tiga ialah y = C1 sinh(kx) + C2 cosh(kx).
Tentunya, pada penjabaran di atas kita bekerja secara terbalik. Dengan memilih suatu fungsi tertentu sejak awal, kita bangun beberapa bentuk persamaan diferensial yang sesuai. Nah, dalam problem matematis maupun fisis pada umumnya, kita diberikan/memperoleh persamaan diferensial terlebih dahulu. Pemecahan PD adalah memperoleh fungsi yang memenuhi PD terkait. Fungsi yang bila disulihkan ke dalam PD memberikan kesamaan yang tepat disebut solusi dari persamaan diferensial.
Persamaan diferensial orde satu sebenarnya dapat dengan mudah diperoleh solusinya, antara lain yang memiliki bentuk seperti ini:
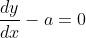
Di mana y = y(x) dan a suatu konstanta. Mula-mula, pindahkan a ke ruas sebelah sehingga suku turunan y'=dy/dx berada di ruas tersendiri.
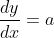
Sekarang, operator dx dapat dipindahkan ke ruas sebelah sehingga menjadi integran.
Dengan mudah dapat diperoleh solusi y = ax + C. Jadi, pada dasarnya kita ingin mengumpulkan antara fungsi dan integrannya (y dan dy) pada satu ruas serta variabel dan integrannya (x dan dx) pada ruas yang lainnya agar kita dapat mengintegralkan keduanya. Dengan pembuktiaan terbalik (seperti metode sebelum-sebelumnya), jelaslah bila y = ax + C maka y’ = a, sehingga y’ – a = 0.
Sekarang kita akan mencoba menyelesaikan PD yang agak lebih rumit. Misalkan kita akan mencari solusi dari PD 4y’ – sin x = 2x.
%5C:&space;dx "\int 4\: dy=\int (\sin x+2x)\: dx")
Hore!!! Kita dapat deh solusinya. Solusi seperti itu dinamakan solusi umum, karena menyisakan suatu konstanta (C) yang tidak kita ketahui nilainya. Nilai dari koefisien C dapat diperoleh melalui syarat-syarat batas. Misalkan diberikan syarat batas y(0) = 5. Dengan menyulihkan nilai x = 0 pada solusi umum di atas, didapatkan,
=-\frac{1}{4}+C=5 "y(0)=-\frac{1}{4}+C=5")
Didapatkan C = 21/4 sehingga diperoleh solusi khusus  "y=\frac{1}{4}(x^2-\cos x+21)")
.
Oke, saya berikan satu contoh terakhir,
Pertama-tama, faktorkan ruas kanan (hingga hanya terdapat satu suku y) kemudian kirim semua y ke ruas kiri dan x ke ruas kanan.
\:&space;dx "\int \frac{dy}{y}=\int (x^2+2)\: dx")
&space;+&space;C_1=\frac{1}{3}x^3+2x&space;+&space;C_2 "\ln (y) + C_1=\frac{1}{3}x^3+2x + C_2")
Akhirnya, didapatkan solusi
 "y=C\cdot\exp\left (\frac{1}{3}x^3+2x \right )")
dengan } "C=e^{(C_2-C_1)}")
adalah suatu tetapan.
Secara umum, PD linear orde-1 dapatlah dinyatakan dalam bentuk umum berikut,
y=Q(x) "\frac{dy}{dx}+P(x)y=Q(x)")
Di sini, kita akan mencari formulasi umum untuk memperoleh solusi dari PD linear orde-1. Mula-mula, kedua ruas dikalikan dengan e∫P(x) dx sehingga
%5C,&space;dx%7D%5Ccdot&space;%5Cfrac%7Bdy%7D%7Bdx%7D+e%5E%7B%5Cint&space;P(x)%5C,&space;dx%7D%5Ccdot&space;P(x)y=e%5E%7B%5Cint&space;P(x)%5C,&space;dx%7D%5Ccdot&space;Q(x) "e^{\int P(x)\, dx}\cdot \frac{dy}{dx}+e^{\int P(x)\, dx}\cdot P(x)y=e^{\int P(x)\, dx}\cdot Q(x)")
Perhatikan bahwa ruas kiri merupakan turunan dari ye∫P(x) dx sehingga
%5C,&space;dx%7D&space;%5Cright&space;)=e%5E%7B%5Cint&space;P(x)%5C,&space;dx%7D%5Ccdot&space;Q(x) "\frac{d}{dx}\left (ye^{\int P(x)\, dx} \right )=e^{\int P(x)\, dx}\cdot Q(x)")
Akhirnya, kita peroleh formulasi untuk solusi dari PD linear orde-1
%5C,&space;dx%7D%5Cint&space;%5Cleft&space;(e%5E%7B%5Cint&space;P(x)%5C,&space;dx%7D%5Ccdot&space;Q(x)&space;%5Cright&space;)%5C:&space;dx "y=e^{-\int P(x)\, dx}\int \left (e^{\int P(x)\, dx}\cdot Q(x) \right )\: dx")
Demikianlah pengantar dari pengantar persamaan diferensial ini. Setelah memahami konsepnya tentunya buku teks matematika di meja Anda akan terasa lebih menyenangkan untuk dipelajari.
